Learning Distributed Safe Multi-Agent Navigation via Infinite-Horizon Optimal Graph Control

Fenglan Wang, Xinguo Shu, Lei He, Lin Zhao*
National University of Singapore
Department of Electrical and Computer Engineering
*Corresponding Author

Abstract

Distributed multi-agent navigation faces inherent challenges due to the competing requirements of maintaining safety and achieving goal-directed behavior, particularly for agents with limited sensing range operating in unknown environments with dense obstacles. Existing approaches typically project predefined goal-reaching controllers onto control barrier function (CBF) constraints, often resulting in conservative and suboptimal trade-offs between safety and goal-reaching performance. 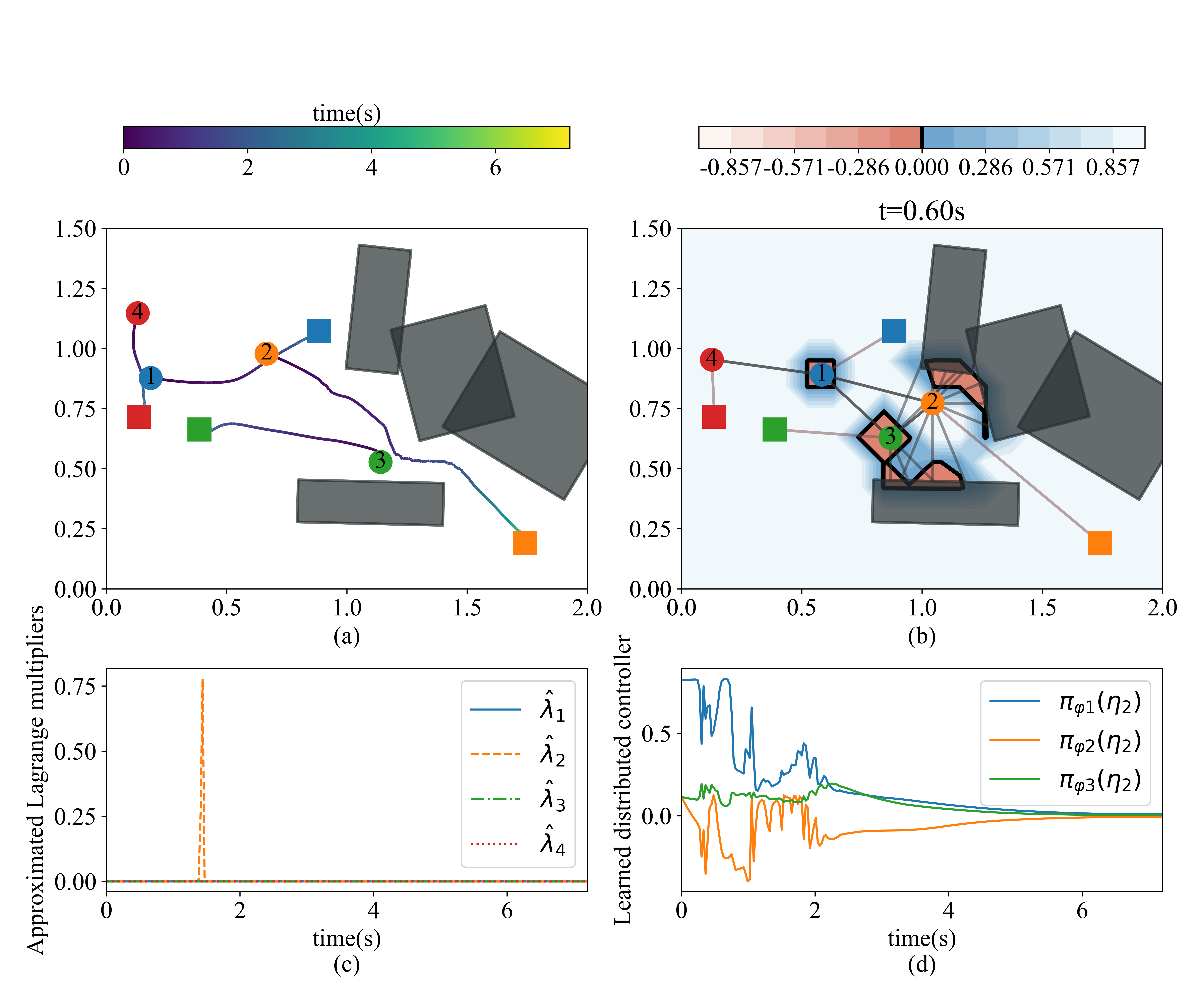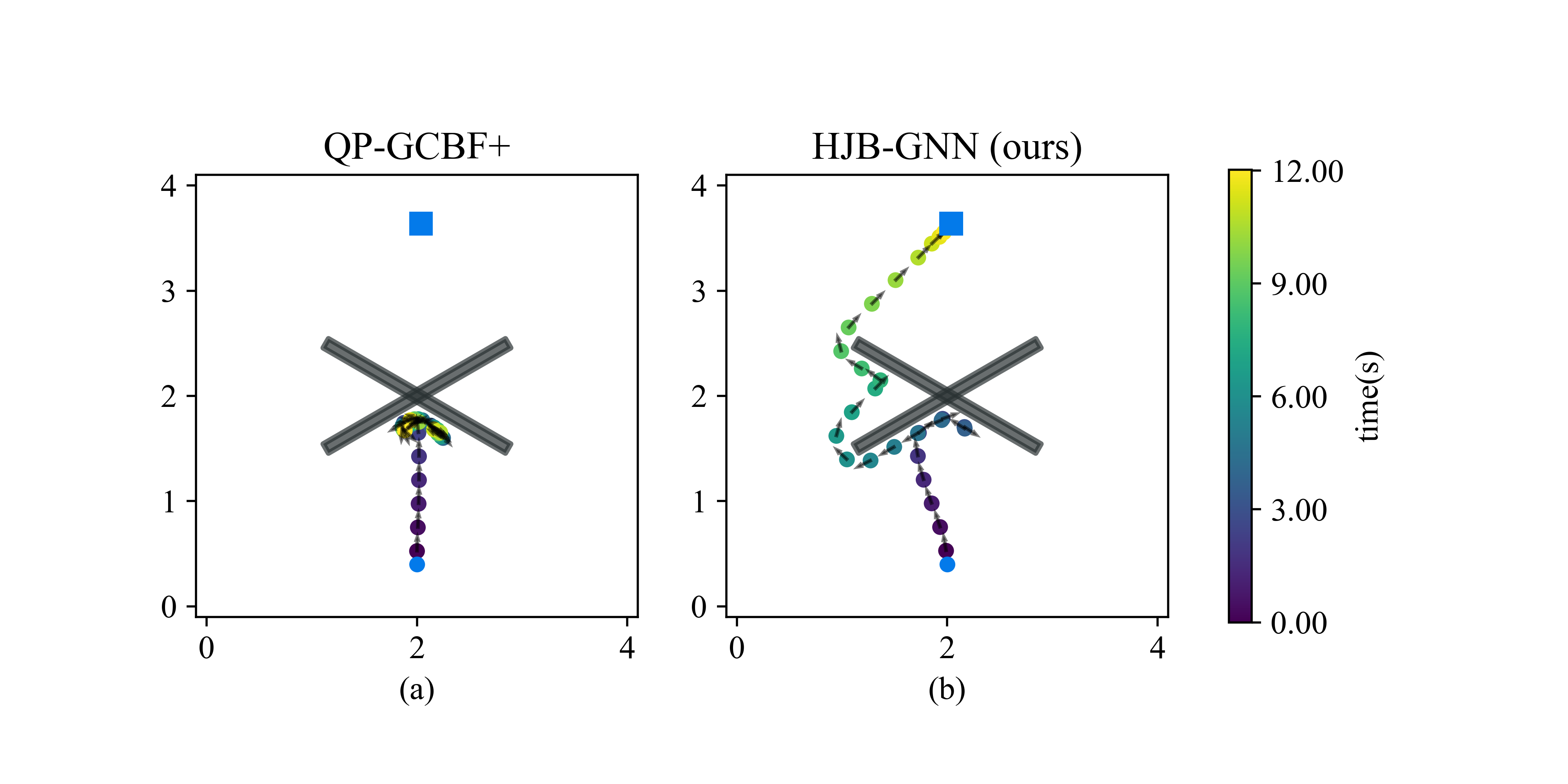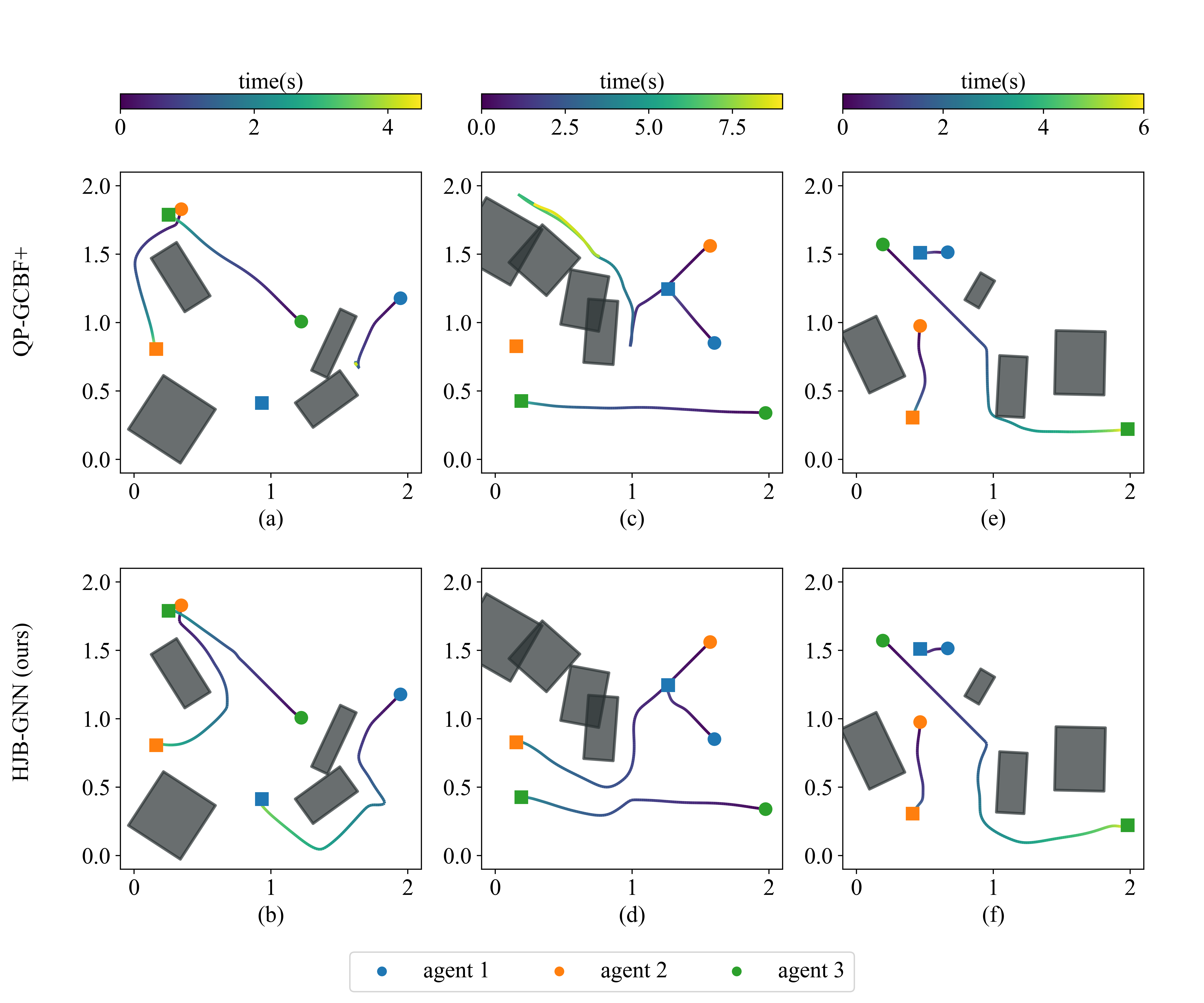We propose an infinite-horizon CBF-constrained optimal graph control formulation for distributed safe multi-agent navigation. By deriving the analytical solution structure, we develop a novel Hamilton-Jacobi-Bellman (HJB)-based learning framework to approximate the solution. In particular, our algorithm jointly learns a CBF and a distributed control policy, both parameterized by graph neural networks (GNNs), along with a value function that robustly guides agents toward their goals. Moreover, we introduce a state-dependent parameterization of Lagrange multipliers, enabling dynamic trade-offs between safety and performance. Unlike traditional short-horizon, quadratic programming-based CBF methods, our approach leverages long-horizon optimization to proactively avoid deadlocks and navigate complex environments more effectively. 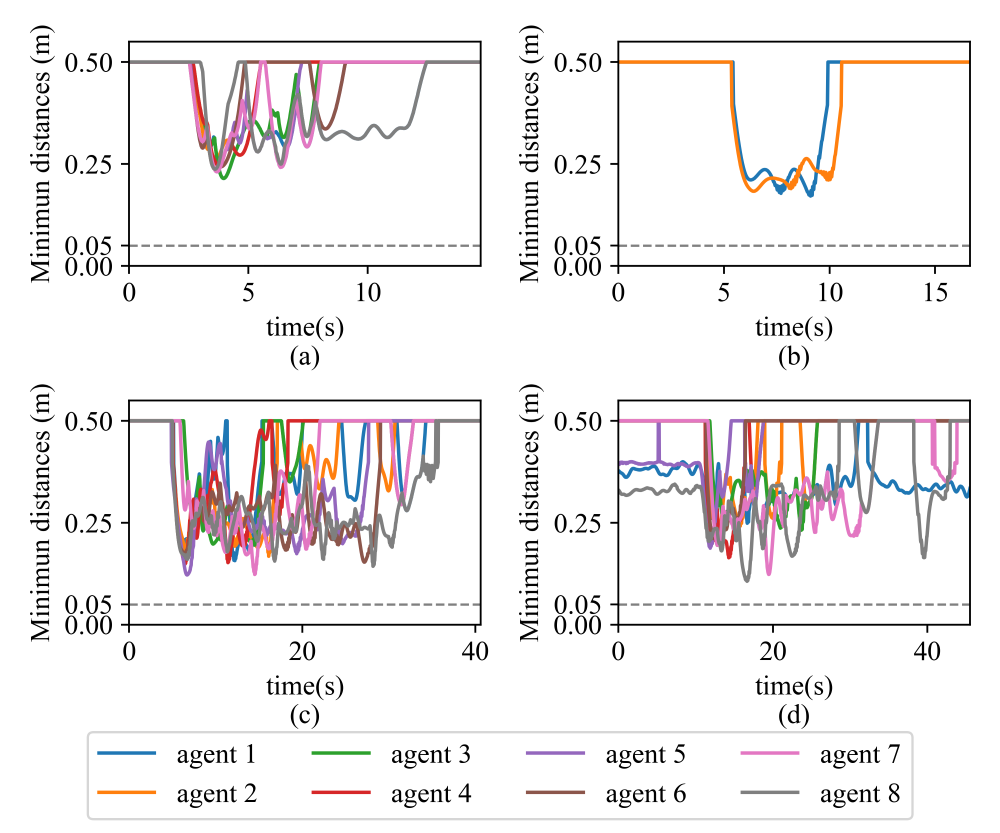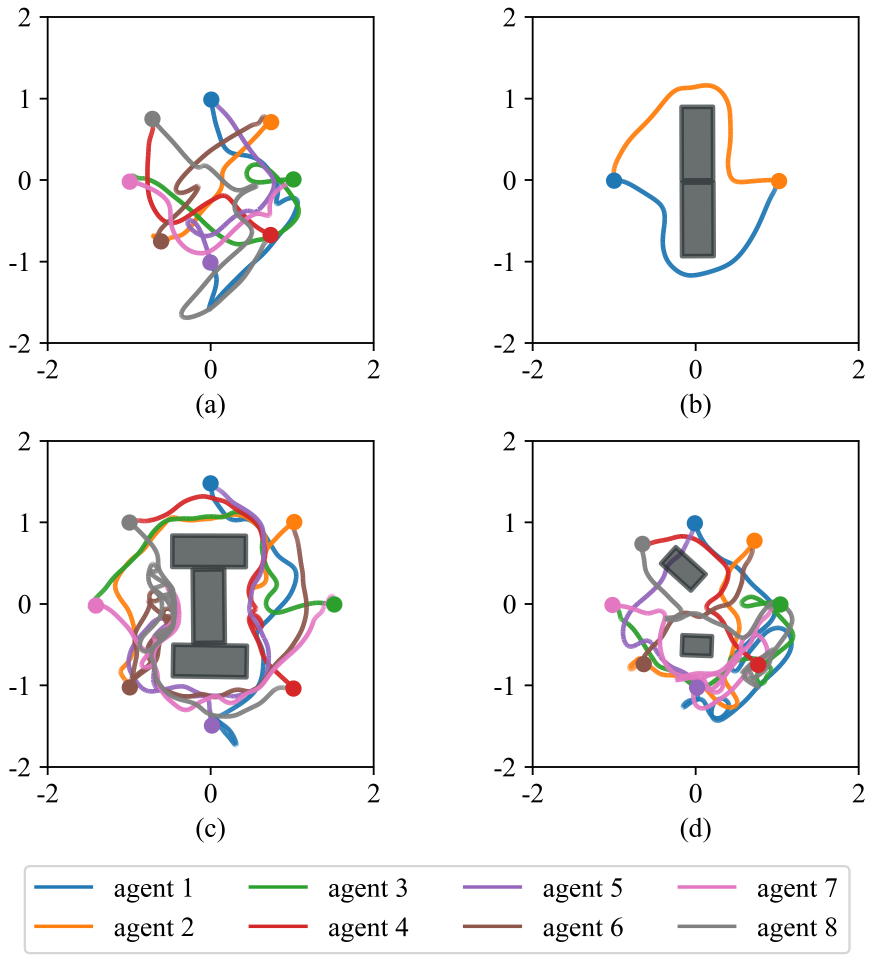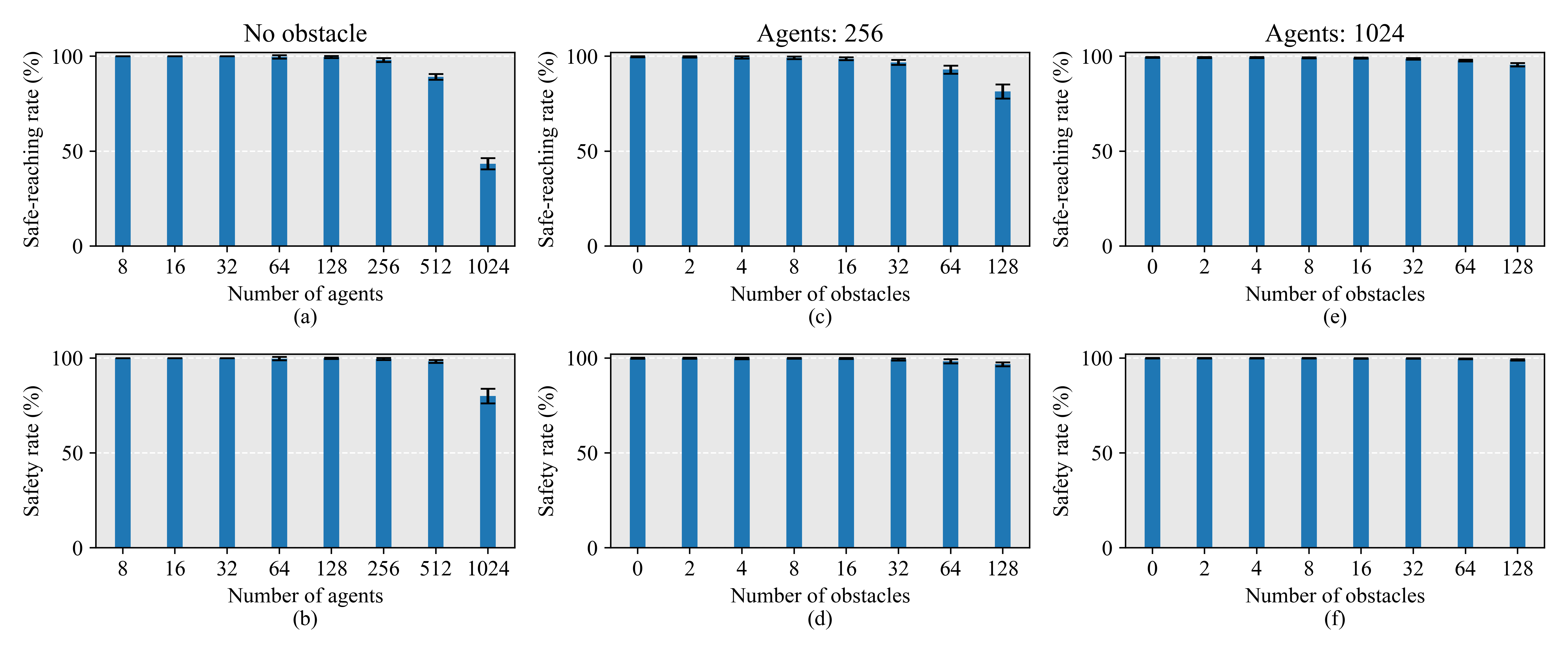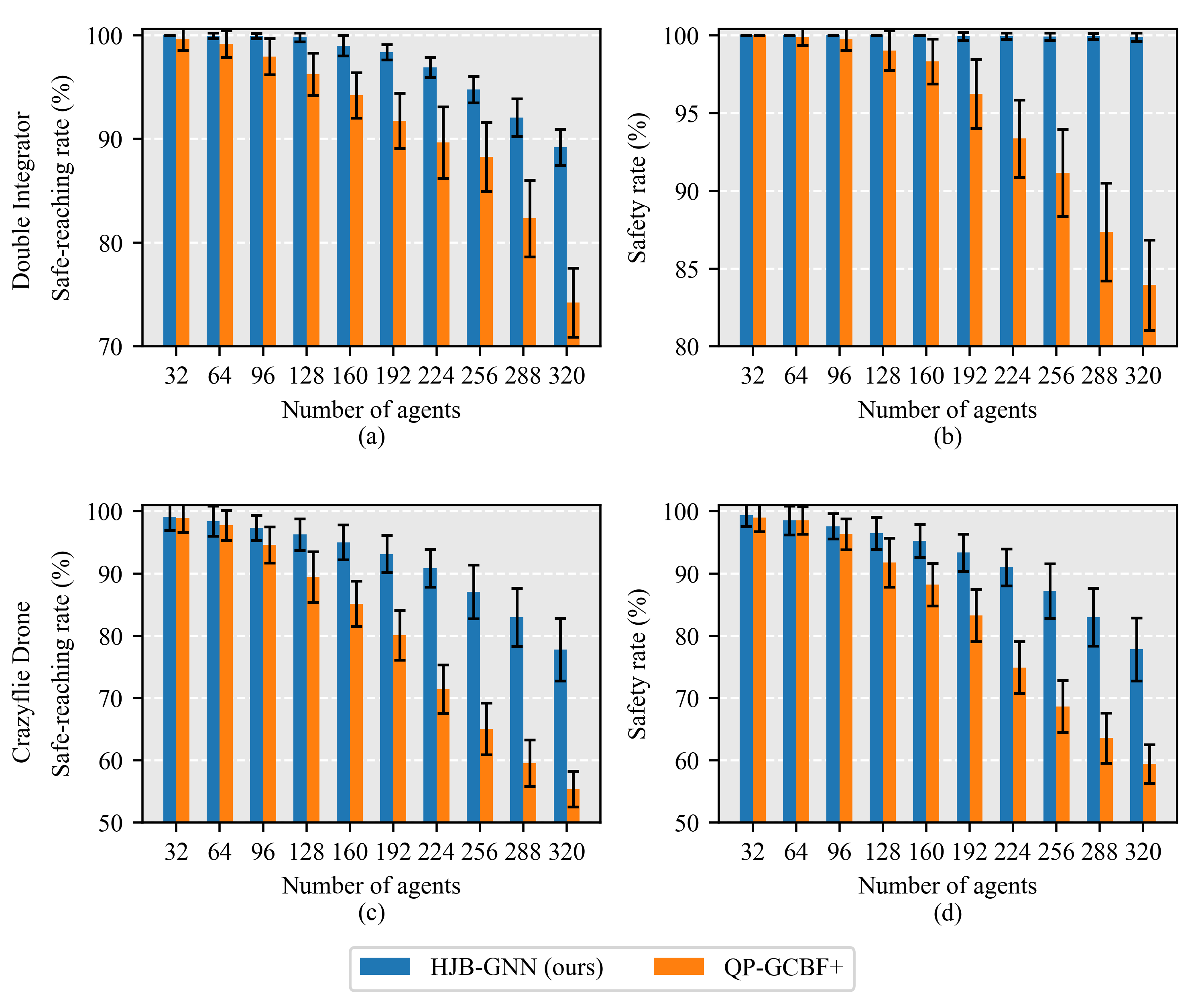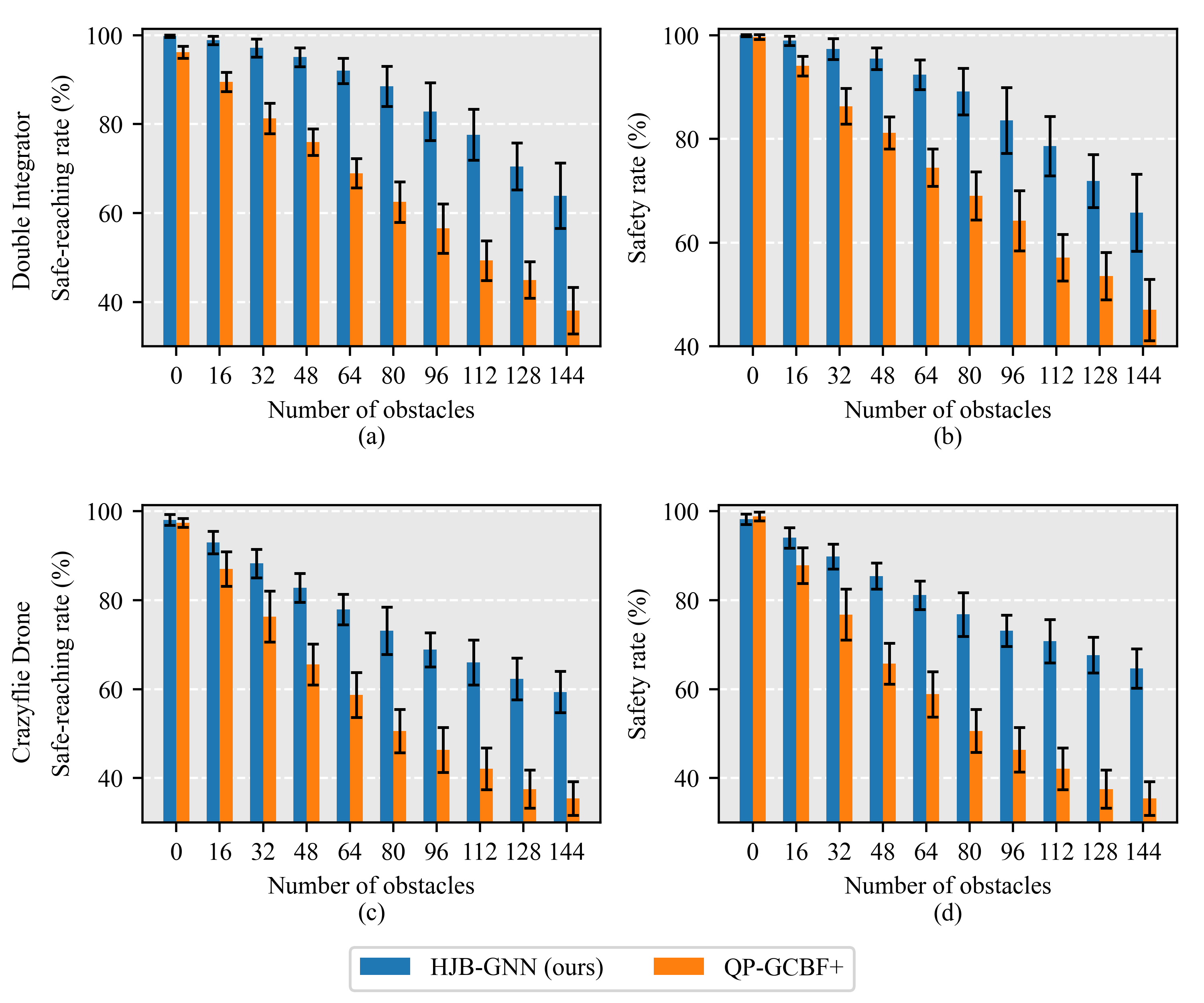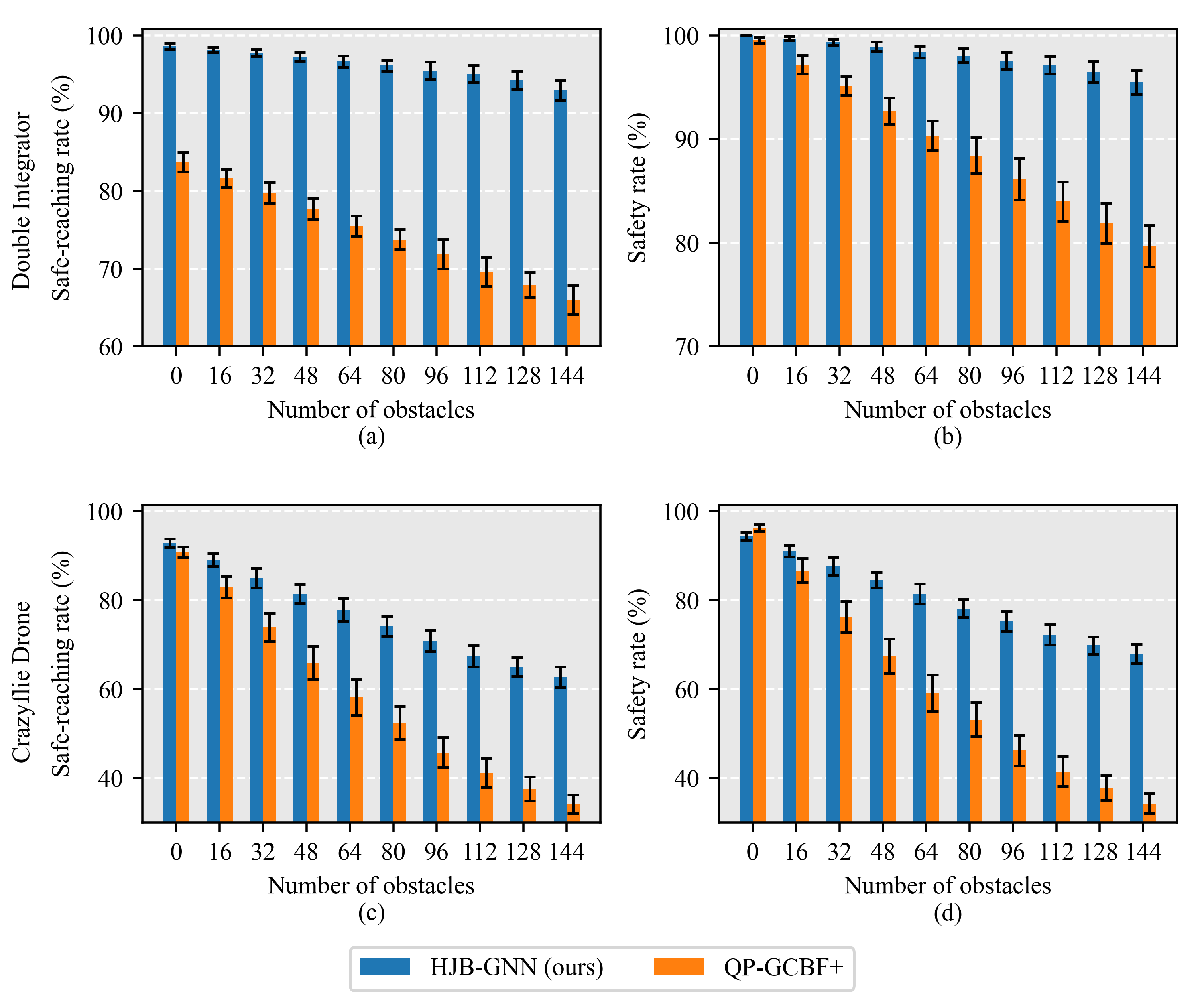Extensive simulation results demonstrate substantial improvements in safety and task success rates across various agent dynamics, with strong scalability and generalization to large-scale teams in previously unseen environments. Real-world experiments using Crazyflie drone swarms on challenging antipodal position-swapping tasks further validate the practicality, generalizability, and robustness of the proposed HJB-GNN learning framework.

Hardware Experiments

fig 5

Fig. 8. Hardware experiment setup for antipodal position-swapping task: (a) 8 Crazyflie drones without obstacle; (b) 2 Crazyflie drones with a long static obstacle; (c) 8 Crazyflie drones with large non-convex static obstacles; (d) 8 Crazyflie drones with both a static obstacle and a large dynamic obstacle mounted on a randomly moving car.





(a) 8 Crazyflie drones without obstacle

(b) 2 Crazyflie drones with a long static obstacle

(c) 8 Crazyflie drones with large non-convex static obstacles

(d) 8 Crazyflie drones with both a static obstacle and a large dynamic obstacle mounted on a randomly moving car





fig 5

Fig. 10. Hardware experiment results: Minimum distances between each agent and other agents or obstacles over time for four sets of experiments under \(r=0.05{\rm m}\), corresponding to scenarios (a)-(d) in Fig. 8, respectively.





fig 5

Fig. 11. Simulation trajectories of all Crazyflie drones correspond to four sets of experiments in Fig. 8. The upper gray rectangle in (d) indicates the initial position of dynamic obstacle in (d) of Fig. 8.





Numerical Simulations

2D environment

agents=128, obstacles=0

agents=512, obstacles=0

agents=1024, obstacles=0

agents=16, obstacles=16

agents=32, obstacles=16

agents=32, obstacles=32

3D environment

agents=64, obstacles=0

agents=128, obstacles=0

agents=512, obstacles=0

agents=32, obstacles=16

agents=64, obstacles=32

agents=128, obstacles=64

All Figures in the Paper

Simulations for the HJB-GNN Learning Approach

fig 2 plot

Fig. 2. Illustration of our HJB-GNN approach on the unmanned surface vessel under 4 agents and 4 static obstacles case in a \(2\,\mathrm{m} \times 1.5\,\mathrm{m}\) region: (a) four agents (numbered circles indicating their initial positions) reach their respective goals (squares with the same color as agents) while avoiding collisions with other agents and static obstacles (gray rectangles), (b) graph CBF contour of agent 2 at \(t=0.6{\rm s}\), (c) approximated Lagrange multipliers \(\hat{\lambda}_i,\ i=1,2,3,4\) of four agents, and (d) learned distributed controller \(\pi_{\varphi}(\eta_2)=[\pi_{\varphi 1}(\eta_2),\pi_{\varphi 2}(\eta_2),\pi_{\varphi 3}(\eta_2)]^T\) of agent 2.





fig 1

Fig. 3. Safe-reaching rates ((a), (c), (e)) and safety rates ((b), (d), (f)) for 2D unmanned surface vessel under fixed area width. (a)-(b): no obstacle with increasing numbers of agents, (c)-(d): 256 agents with increasing numbers of obstacles, and (e)-(f): 1024 agents with increasing numbers of obstacles.





Comparative Simulations

fog 6 plot

Fig. 1. Comparison between QP-GCBF+ of [32] in (a) and our HJB-GNN in (b). An agent (a gradient-colored circle) aims to reach the goal (blue square) while avoiding static obstacles (gray rectangles) within a \(4{\rm m}\times4{\rm m}\) region. The black arrow indicates the velocity direction of agent. The QP-GCBF+ has deadlock near obstacles, and our HJB-GNN approach achieves goal-reaching without collision.


fig 7

Fig. 4. Comparisons between the QP-GCBF+ method ((a), (c), and (e)) in [32] and our HJB-GNN approach ((b), (d), and (f)) under three cases with four agents (circles indicating their initial positions) and four static obstacles (gray rectangles) in a \(2{\rm m}\times2{\rm m}\) region. Agent 1 in (a) and agent 2 in (c) experience deadlock, and agent 3 in (e) collides with an obstacle. All agents safely reach their respective goals (squares with the same colors as agents) in (b), (d), and (f).





fig 3

Fig. 5. Safe-reaching rates and safety rates for increasing numbers of agents and no obstacle under fixed area width. (a)-(b): 2D double integrator, and (c)-(d): 3D Crazyflie drone.





fig 4

Fig. 6. Safe-reaching rates and safety rates for increasing numbers of obstacles and 256 agents under fixed area width. (a)-(b): 2D double integrator, and (c)-(d): 3D Crazyflie drone.





fig 5

Fig. 7. Safe-reaching rates and safety rates for increasing numbers of obstacles and 1024 agents under fixed area width. (a)-(b): 2D double integrator, and (c)-(d): 3D Crazyflie drone.